- Joined
- Sep 14, 2011
- Messages
- 2,676
- Reaction Score
- 6,257
No, not the Dee/Maya/Stewie GOAT problem. The other -- lower case o-a-t, as in the animal -- Goat problem.
To be 100% honest, I wasn't aware of any goat-the-animal problem, infamous, famous, or otherwise, until I read the below link. And, as long as I'm being honest, I can't say I understand whatever they're claiming is a solution either. The only reason I'm bringing it up here is because there's a reference to Zeno's Paradox which I did solve many years ago but which still trips up many of the scientifically/mathematically minded today, and I'm wondering if others here have spent time solving it on their own.
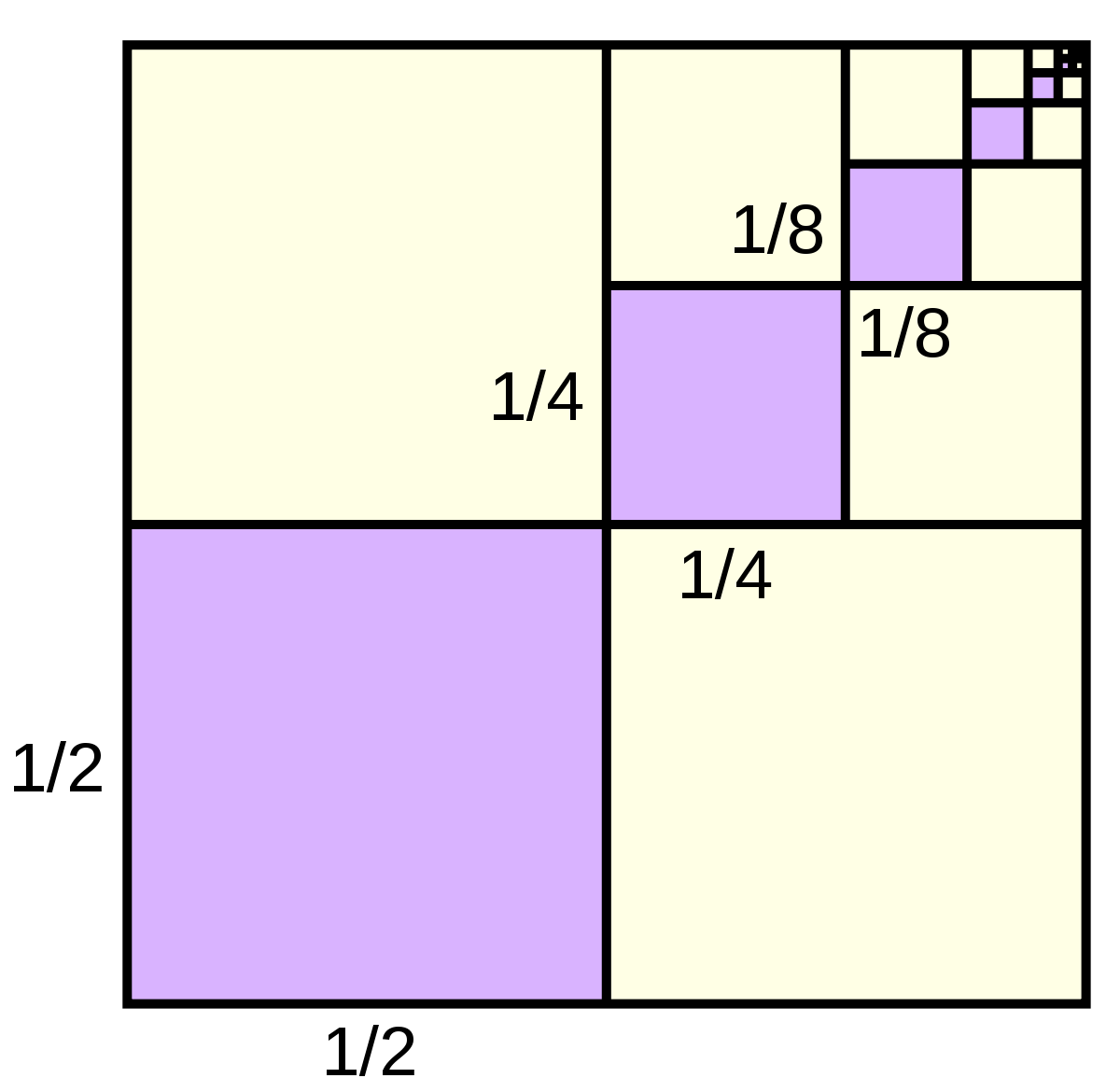
Zeno's Paradox has been posited in many forms. I first began pondering it in the form of a hypothetical ball that, when released from a height (the actual distance isn't materially important), strikes a surface and rebounds to exactly one-half the height from which it was dropped. The ball then falls from that new height and rebounds to half again. This continues ad infinitum, the ball always bouncing exactly half as high. The question, and ensuing paradox, is how long will the ball bounce. Again, this is a hypothetical ball. There's no friction or heat dissipation or atmospheric resistance or uncertainty principal to confound things. Just pure mathematics. The quick answer, the obvious answer, and the wrong answer (even in the hypothetical world) is it won't, i.e., the ball will continue bouncing forever. Anybody know why the ball will stop? I learned the reason in about 6th grade arithmetic when I was introduced to decimals but didn't learn of Zeno and his paradox until 15 or so years later.

 finance.yahoo.com
finance.yahoo.com
To be 100% honest, I wasn't aware of any goat-the-animal problem, infamous, famous, or otherwise, until I read the below link. And, as long as I'm being honest, I can't say I understand whatever they're claiming is a solution either. The only reason I'm bringing it up here is because there's a reference to Zeno's Paradox which I did solve many years ago but which still trips up many of the scientifically/mathematically minded today, and I'm wondering if others here have spent time solving it on their own.
Zeno's Paradox has been posited in many forms. I first began pondering it in the form of a hypothetical ball that, when released from a height (the actual distance isn't materially important), strikes a surface and rebounds to exactly one-half the height from which it was dropped. The ball then falls from that new height and rebounds to half again. This continues ad infinitum, the ball always bouncing exactly half as high. The question, and ensuing paradox, is how long will the ball bounce. Again, this is a hypothetical ball. There's no friction or heat dissipation or atmospheric resistance or uncertainty principal to confound things. Just pure mathematics. The quick answer, the obvious answer, and the wrong answer (even in the hypothetical world) is it won't, i.e., the ball will continue bouncing forever. Anybody know why the ball will stop? I learned the reason in about 6th grade arithmetic when I was introduced to decimals but didn't learn of Zeno and his paradox until 15 or so years later.
A Mathematician Has Finally Solved the Infamous Goat Problem
It only took a couple centuries.
Last edited: